Schmitt, Stefan

1994 La problemática en la determinación de edad y estatura a partir de restos óseos de poblaciones Mayas. En VII Simposio de Investigaciones Arqueológicas en Guatemala, 1993 (editado por J.P. Laporte y H. Escobedo), pp.23-33. Museo Nacional de Arqueología y Etnología, Guatemala.

4 LA PROBLEMÁTICA EN LA DETERMINACIÓN DE

EDAD Y ESTATURA

A PARTIR DE RESTOS ÓSEOS DE POBLACIONES MAYAS

Stefan Schmitt

Desde el mes de julio de 1992 el Equipo de Antropología Forense de Guatemala ha estado realizando exhumaciones de los denominados «cementerios clandestinos» en distintas partes de la república. La finalidad de dichas exhumaciones y su documentación como su estudio científico, es la identificación. Identificando el hecho, ocurrido clandestinamente en un pasado reciente y a las personas quienes fueron víctimas de estos hechos.

La identificación de las víctimas se hace en base de la individualización de sus restos óseos. Los siguientes criterios se utilizan para lograr esta individualización:

Raza
Sexo
Edad
Estatura
Lateralidad
Uso de tabaco
Patologías (dentales como generales)

Tomados en conjunto, estos criterios proporcionan un cuadro, que se compara con los datos antemortem, los cuales se componen de dos categorías:

1. Los datos que sólo se pueden obtener por entrevistas con familiares que están en búsqueda de un familiar desaparecido, como lateralidad, fumador, patologías, oficio, etc.

2. Datos como edad y estatura, que en muchos casos pueden ser recuperados de los archivos de la iglesia y de los registros civiles.

La identificación de un esqueleto se logra cuando los datos antemortem concuerdan con los datos derivados de los restos óseos.

De todos los criterios mencionados anteriormente, sólo dos varían según la población estudiada: la edad y la estatura. Todos los esqueletos cuyos datos se presentan aquí, pertenecen a individuos de la población y cultura indígena de Guatemala.

En seguida se discuten los diferentes métodos y las fórmulas que generalmente se utilizan para la determinación de estatura a partir de restos óseos.

Un problema que se ha presentado es la verificación de dichos métodos. Además, hasta ahora no hay un método que se base en las características específicas de crecimiento humano de poblaciones indígenas de Guatemala.

La finalidad de esta ponencia es de presentar y discutir los resultados de varios métodos de determinación de estatura que fueron aplicados a 17 esqueletos completos provenientes de algunos cementerios clandestinos exhumados por el Equipo de Antropología Forense de Guatemala.

MATERIALES Y MÉTODOS

Varias fórmulas para la determinación de estatura a partir de restos óseos fueron aplicadas a 17 esqueletos masculinos provenientes de cementerios clandestinos de San José Pacho y Tunaja, Quiché y de Chichupac, Baja Verapaz.

De un total de 69 esqueletos, sólo 17 fueron incluidos en este estudio por haber sido identificados y porque se logró obtener sus estaturas en vida del registro civil.

A estos esqueletos se aplicaron las distintas fórmulas para la determinación de restos óseos a partir del largo máximo del fémur. Las fórmulas de siguientes estudios hechos en el pasado fueron aplicados:

1. Las fórmulas que fueron desarrolladas para mongoloides y mexicanos en 1958 por Trotter y Gleser en base de restos óseos de individuos muertos en la guerra de Corea.

2. Una fórmula que fue desarrollada por Genovés en 1967 en base de cadáveres de la población mexicana.

3. Una fórmula desarrollada por Fully en 1956 en base de restos óseos de individuos franceses deportados que habían muerto durante la guerra.

Dentro de estos métodos, se utilizaron para la muestra de los 17 esqueletos guatemaltecos las fórmulas de determinación de estatura a partir del largo máximo del fémur, por la razón de que este hueso se encuentra por lo general en el mejor estado de preservación. Cada fórmula arroja como resultado un punto medio de estatura, del cual se deriva el rango de estatura con la desviación estándar dada por cada uno de los métodos.

De una muestra de 68 hombres de la población mongoloide norteamericana, muertos en la guerra de Corea, Trotter y Gleser desarrollaron 1958 la siguiente formula utilizando el largo máximo del fémur (Stewart 1979:201-202):

(2.15 x largo máximo de fémur) + 725.7 milímetros

Desviación estándar: +/- 38.0 milímetros

(Krogman 1986:310)

La segunda que se aplicó es la desarrollada por ellos a partir de una muestra de 63 individuos mexicanos masculinos, también muertos en la guerra de Corea (Stewart 1979:201-202):

(2.40 x largo máximo del fémur) + 586.7 milímetros

Desviación estándar: +/- 29.9 milímetros

(Krogman 1986:310)

La tercera formula para la estimación de estatura es la desarrollada por Genovés a partir de una muestra de cadáveres de la población mexicana en 1966. Más tarde ésta fue corregida, en tanto que sólo tomó en cuenta los cadáveres pertenecientes a indígenas, reduciendo la muestra a sólo 22 individuos masculinos y 15 femeninos (Krogman 1986:318-319). La fórmula desarrollada para hombres es la siguiente:

(2.26 x largo máximo del fémur) + 638.79 milímetros

Desviación estándar: +/- 34.17 milímetros

(Bass 1987:29)

Por último, se aplicó el método desarrollado por Fully en 1956 en base de restos óseos de franceses que habían sido deportados a Austria donde murieron durante la segunda guerra mundial y donde fueron enterrados cerca de un campo de concentración en Mauthausen. De 3165 esqueletos recuperados, sólo 102 fueron identificados para los cuales se logró recuperar estaturas en vida. De estos se desarrolló un método de determinación de estatura a partir de todos los huesos que contribuyen a la estatura de un individuo, la llamada estatura ósea.

Las medidas utilizadas para la estatura ósea son las siguientes:

Cráneo: altura medida entre el basión y el bregma
Vértebras: altura de los cuerpos de las vértebras C2 hasta L5
Segmento 1 del sacro: altura medida desde la cara anterior
Fémur: largo bicondilar
Tibia: largo entre superficie articular proximal y distal
Talo y calcáneo en posición articulada: altura entre superficie articular tibio-talar y la parte más distal del calcáneo.

Luego, para estaturas óseas menos de 153.5 cm se suma un factor correccional (el tejido blando que contribuye a la estatura de una persona) de 10.0 cm. Para estaturas óseas entre 153.6 y 165.4 cm se suma el factor correccional de 10.5 cm. Un factor de 11.5 cm se suma a las estaturas óseas mayores de 165.5 cm. A los resultados se aplica un rango máximo de error de

+/- 3 cm (Stewart 1979:218-221).

En la muestra de los 17 esqueletos exhumados por el Equipo de Antropología Forense de Guatemala, sólo a 14 casos se pudo aplicar el método de Fully. A los otros tres algunas medidas no se pudieron tomar por su mal estado de preservación.

Dentro de las estaturas óseas medidas en la muestra de esqueletos guatemaltecos, ninguno sobrepasó una estatura de 153.5 cm. Por lo tanto, en los casos donde se aplicó este método se sumó el factor correccional de 10.0 cm a la estatura ósea.

Para poder verificar los rangos de estatura calculadas, aplicando las fórmulas mencionadas a la muestra guatemalteca, las estaturas en vida obtenidas del registro civil, sirvieron como criterio de comparación.

Ahora, un factor que se tiene que incluir es el crecimiento que se da después de los 18 años de edad, cuando se tomaron las estaturas en el registro civil.

Para eso, se recurrió a los estudios que se llevaron a cabo por el Dr. Barry Bogin en colaboración con la Universidad del Valle de Guatemala. Dentro de dicho estudio se compararon tres muestras de niños de diferentes clases socioeconómicos. La primera representando a niños indígenas de una área rural, la segunda de niños clasificados por su orientación cultural como ladinos de una clase socioeconómica baja y la tercera de una clase socioeconómica alta, también clasificada como ladina.

El estudio da de entender de que «En términos prácticos la demora relativamente más tardada en el crecimiento que en maduración ósea de los niños de la clase socioeconómica baja significa que es probable que vayan ser bastante más pequeños en estatura y más livianos en peso, que los niños de la

clase socioeconómica alta en todas las edades y que quedan más chaparros como adultos» (Bogin et al 1989:112).

Además consta que «Comparaciones de datos de crecimiento recogidos en los años 1960 y los años 1980, muestran que niños indígenas no han tenido cambios significativos en estatura o peso en los últimos 25 años» (Bogin et al 1989).

Concluyendo, dice que el déficit de crecimiento en clases socioeconómicas bajas, como la población indígena guatemalteca, es debido a las malas condiciones nutricionales y médicas en las que se encuentran dichas poblaciones (Bogin et al 1989). Tampoco es probable que haya habido grandes cambios en dicho ambiente en el pasado.

Por lo tanto se puede afirmar que el crecimiento en estatura en la población indígena sigue después de los 18 años. En comunicación personal (1993) con el Dr. Bogin, él afirmó que este crecimiento probablemente sigue hasta los primeros años de los 20.

Este hecho es debido a la tardanza en la maduración ósea, es decir la fusión de las epífisis con las diáfisis de los huesos largos y es debido a desnutriciones y enfermedades crónicas, entre otras cosas (Bogin 1988:38).

De estos estudios surge la necesidad de llegar a un factor correccional en crecimiento después de los 18 años para la población indígena guatemalteca, que se tiene que sumar a la estatura medida por el registro civil.

En discusión con el Dr. Bogin y en vista de un estudio llevado a cabo en una población polaca donde la gente creció aproximadamente 2.13 cm después de los 19 años (Bogin 1988:38), se decidió utilizar para la población indígena guatemalteca un valor correccional de 2.5 cm.

Este factor de 2.5 cm fue sumado a la estatura que se obtuvo del registro civil para la muestra de los 17 individuos del presente estudio. En adelante se referirá a ésta como la estatura en vida.

MÉTODOS ESTADÍSTICOS

Con estos datos se calculó para cada individuo de la muestra el punto medio y el rango de estatura. El último por medio de la desviación estándar dado en las formulas de Trotter y Gleser y en la de Genovés. El rango de estatura en la formula de Fully se derivó a partir de un rango máximo de error dado por el autor (Stewart 1979:219).

Luego se visualizaron los resultados en gráficas de barra por medio del programa Lotus 1-2-3, la estatura mínima y máxima (el rango de estatura) respectivamente a la izquierda y derecha de la estatura en vida del individuo para cada una de las fórmulas.

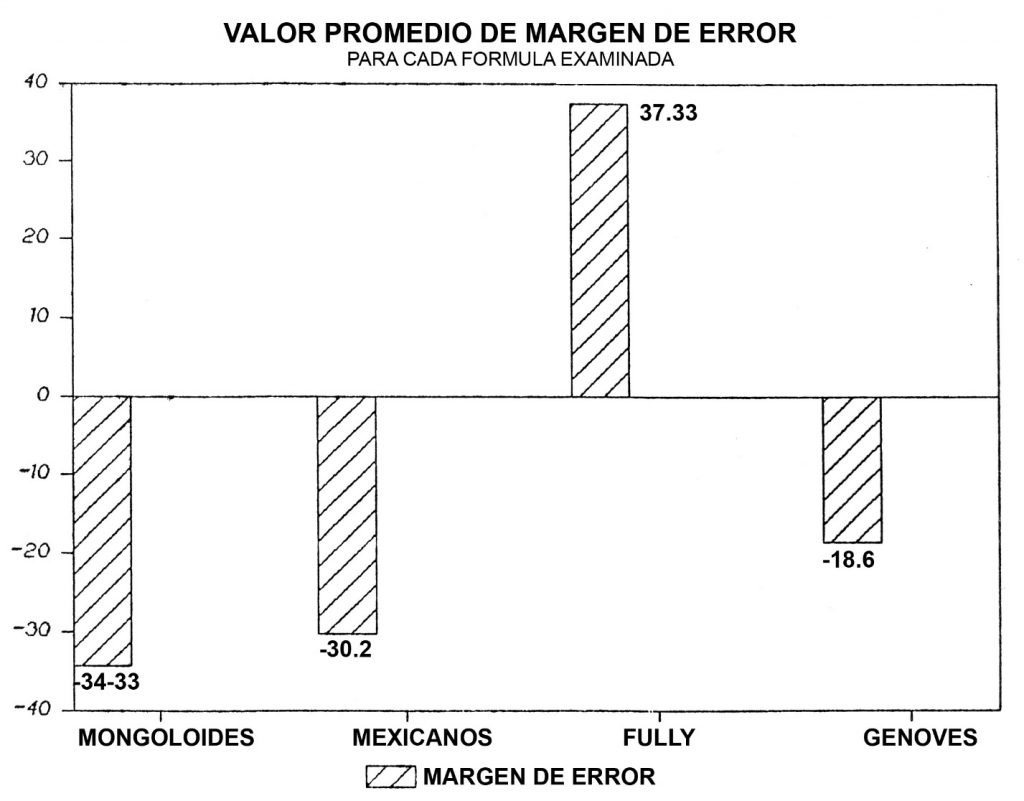
Para poder calcular el margen de error de cada una de las fórmulas, se procedió a sustraer de la estatura en vida el punto medio determinado por las fórmulas dando 17 resultados. Estos se sumaron y para obtener un valor promedio de margen de error, fueron divididos por 17.

Dicho valor promedio arrojado para cada fórmula examinada, indica si la formula respectiva tiende a subestimar o sobreestimar la estatura y hasta que grado lo hace.

RESULTADOS

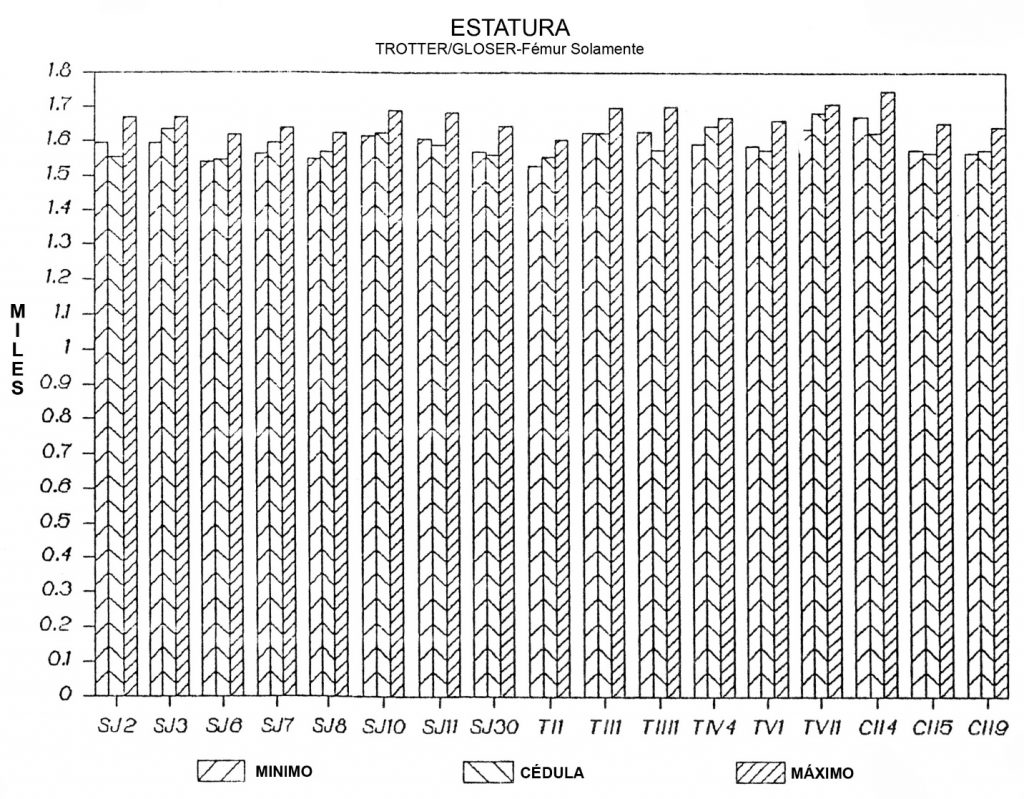
1. LA FÓRMULA DE TROTTER Y GLESER PARA MONGOLOIDES A PARTIR DEL LARGO MÁXIMO DEL FÉMUR (Figura 1)

Viendo la gráfica, se puede ver que 10 de 17 casos caen dentro de los rangos determinados con la fórmula para mongoloides a partir del largo máximo del fémur. Representado este resultado en porcentajes, es un valor aproximado de sólo 59%.

Ahora, el valor promedio de margen de error (determinado sustrayendo de la estatura en vida el punto medio calculado por la fórmula) es de -34.33 mm. Es decir que la fórmula para mongoloides de Trotter y Gleser tiende a sobreestimar la estatura del individuo por un valor promedio aproximado de 3.4 cm.

Figura 1 Estatura Trotter/Gleser, fémur solamente

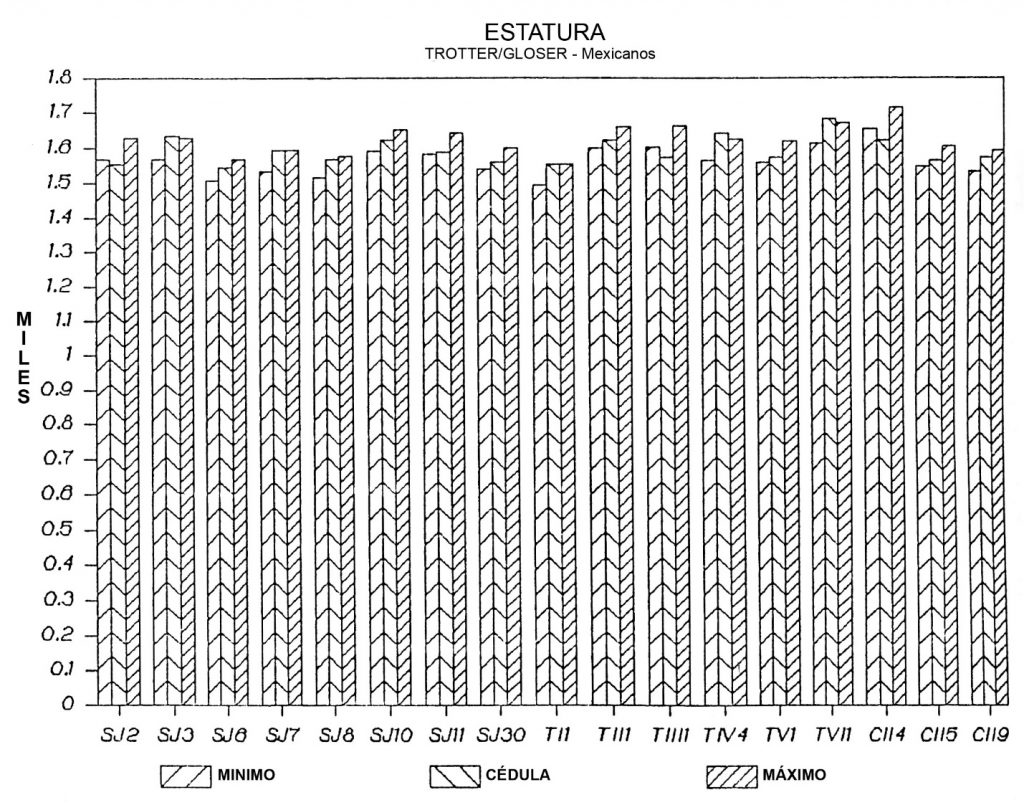
2. LA FÓRMULA DE TROTTER Y GLESER PARA MEXICANOS A PARTIR DEL LARGO MÁXIMO DEL FÉMUR (Figura 2)

La gráfica muestra que el resultado, comparado con la fórmula anterior, es el mismo. También 10 de 17 casos caen dentro de los rangos, con la diferencia de que cuatro rangos que anteriormente fueron correctos ahora subestiman la estatura en vida y cuatro en donde antes dicha estatura cayó poco debajo del margen mínimo del rango, ahora encajaron bien en los nuevos rangos. Así es que también 10 de 17 casos caen dentro de los rangos calculados, aunque en algunos casos éstos son diferentes a los de la anterior fórmula. Otra vez aquí, solamente un aproximado 59% de los casos cayeron en los rangos calculados.

El valor promedio de margen de error es de -30.2 mm. Es decir que la fórmula para mexicanos de Trotter y Gleser tiende a sobreestimar la estatura del individuo por un valor promedio aproximado de 3 cm que es menor que la sobrestimación ocurrida en la fórmula para mongoloides.

Figura 2 Estatura Trotter/Gleser, mexicanos

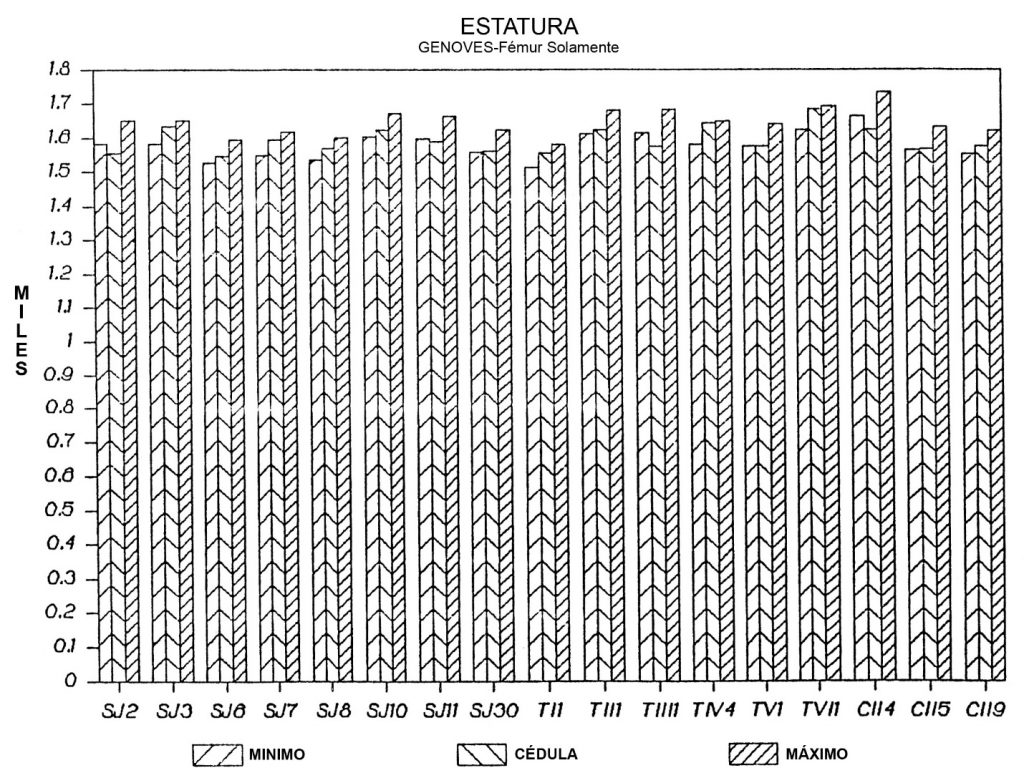
3. LA FÓRMULA DE GENOVÉS PARA LA DETERMINACIÓN DE ESTATURAS DE INDÍGENAS MEXICANOS (Figura 3)

Viendo la gráfica, se puede ver que 12 de 17 casos caen dentro de los rangos calculados. En porcentajes equivale a aproximadamente 70%. Comparado con las fórmulas anteriores, el resultado es mucho mejor. Así también el valor promedio de margen de error para esta fórmula es más pequeño que los anteriormente presentados. La fórmula de Genovés tiende a sobreestimar la estatura en vida de los individuos por un valor promedio de aproximadamente 1.86 cm.

Figura 3 Estatura Genovés, fémur solamente

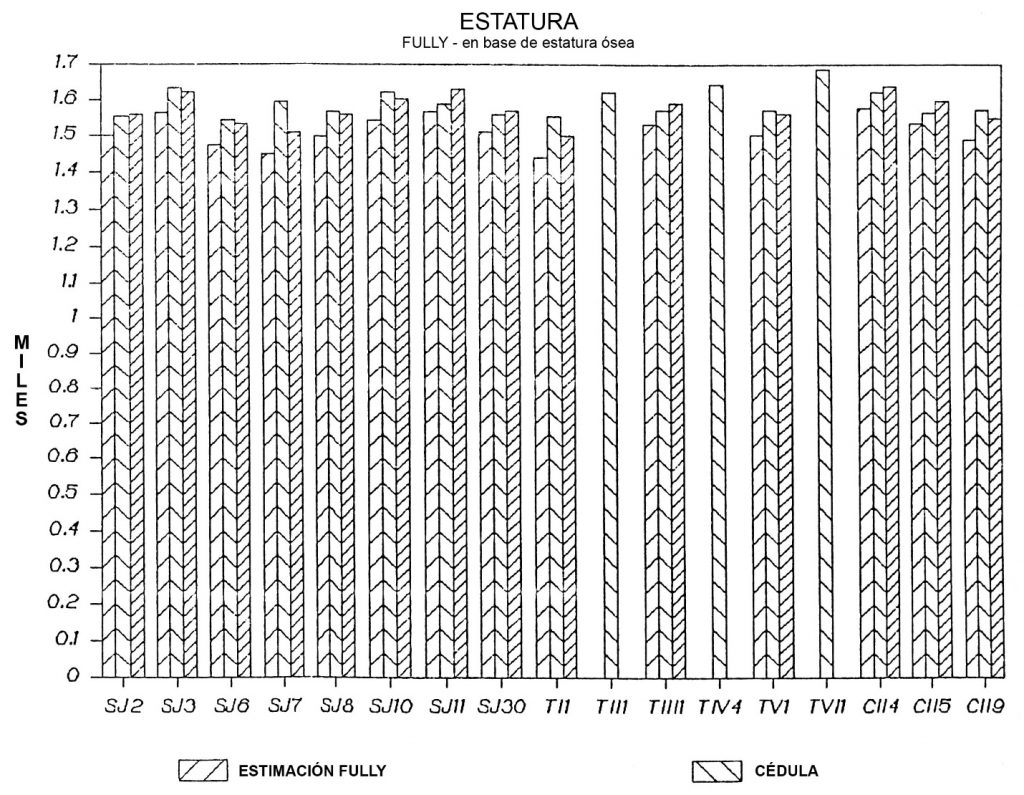
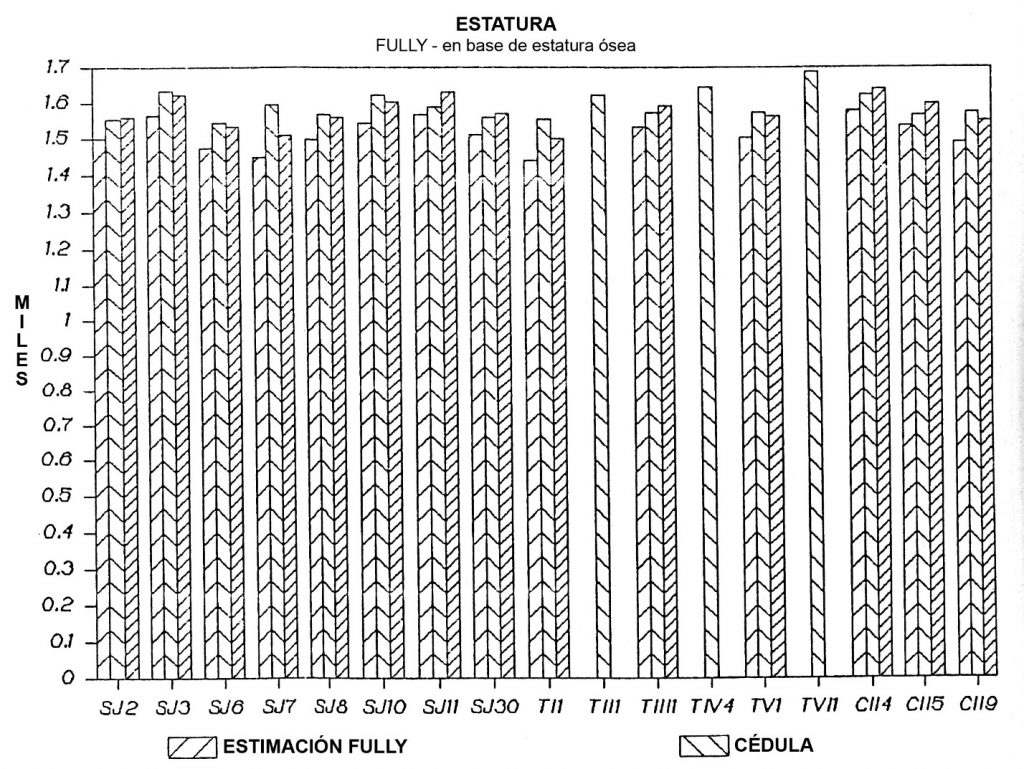
4. LA FÓRMULA DE FULLY PARA LA DETERMINACIÓN DE ESTATURA A PARTIR DE LA ESTATURA ÓSEA (Figura 4)

Como anteriormente mencionado, sólo se podía evaluar esta fórmula con una muestra de 14 individuos. Los rangos calculados se basan en el margen máximo de error de 3 cm hacia arriba y abajo encontrado empíricamente y no estadísticamente como en las fórmulas anteriores, por Fully. En la muestra estudiada por él, 65% de los casos cayeron en un rango que varía sólo 1 cm hacia arriba y abajo del punto medio determinado por su fórmula (Stewart 1979:219).

Como se puede ver en la gráfica, sólo 6 de 14 casos cayeron dentro de los rangos máximos de 3 cm dados por el autor, o sea sólo un 43% de los casos. Los casos que no encajaron, fueron subestimados en respeto a su estatura en vida. En lo referente al valor promedio de margen de error calculado, se puede ver que es el único que subestima la estatura en vida de los individuos incluidos en este estudio por un valor promedio de aproximadamente 3.7 cm (Figura 5).

Figura 4 Estatura Fully, en base a estatura ósea

Figura 5 Valor promedio de margen de error

SUGERENCIAS PARA ESTUDIOS FUTUROS

La pregunta que ahora surge es: ¿Por qué existen estas diferencias entre las fórmulas examinadas? No se puede dar una respuesta conclusiva, pero hay ciertas variaciones en los estudios hechos por los distintos científicos que podrían ser la razón de estas diferencias. Los siguientes puntos son más de carácter especulativo que conclusiones científicas, pero podrían ser tomados en cuenta para estudios futuros:

1. Los estudios hechos por Trotter y Gleser, como los de Fully fueron hechos en base de restos óseos, para los cuales se obtuvieron las estaturas en vida de registros militares. Probablemente estas estaturas de vida fueron tomadas a los 18 años y es posible que no se tomara en cuenta el crecimiento que ocurre después de esta edad.

2. La sobreestimación de estaturas por las fórmulas de Trotter y Gleser y la subestimación de las mismas por la fórmula de Fully podrían ser resultado de un crecimiento diferencial entre las poblaciones norteamericanas (mongoloides y mexicanos) y europeas durante el tiempo en que se hicieron dichos estudios.

3. Por lo tanto, el éxito parcial de la fórmula desarrollada por Genovés podría ser resultado del hecho de que sus estaturas se derivaron directamente de cadáveres y no de un registro, así reflejando la estatura exacta que tenía el individuo al momento de morir.

APRECIACIONES GENERALES

En conclusión se pueden notar varios puntos:

1. La fórmula con los peores resultados es la desarrollada por Fully en 1956, con un éxito de sólo 43% de los casos cayendo en los rangos de estatura calculados con esta fórmula. Además, es la única que subestima la estatura en vida con un valor promedio de margen de error de 3.7 cm, siendo el margen (como valor absoluto) más grande de todas las fórmulas examinadas.

2. Como factor correccional para la fórmula de Fully, se sugiere sumar, en vez de los 10.0 cm dados por el autor, 13.7 cm. Los resultados, como se puede ver en la gráfica (Figura 6), muestran que ahora 71% de los casos caen dentro de los rangos calculados con el nuevo factor correccional.

3. La fórmula que ha proporcionado los mejores resultados en determinar la estatura en vida a partir de restos óseos es la desarrollada por Genovés en 1967. Dicha fórmula tiene el más alto porcentaje de éxito (70%) en referencia a rangos de estatura calculados con ella y el valor promedio de margen de error más pequeño de 1.86 cm.

Figura 6 Estatura Fully, fórmula corregida

REFERENCIAS

Bass, William M.

1987 Human Osteology. Special Publication of the Missouri Archeological Society, Columbia.

Bogin, Barry

1988 Patterns of Human Growth. Cambridge University Press. Cambridge.

Bogin, Barry, Timothy Sullivan, Roland Hauspie y Robert B. Macvean

1989 Longitudinal Growth in Height, Weight, and Bone Age of Guatemalan Ladino and Indian Schoolchildren. American Journal of Human Biology 1:103-113.

Krogman, Wilton M.

1986 The Human Skeleton in Forensic Medicine. Charles C. Thomas Publisher. Springfield, Illinois.

Stewart, T.D.

1979 Essentials of Forensic Anthropology. Charles C. Thomas Publisher. Springfield, Illinois.

4

LA PROBLEMÁTICA EN LA DETERMINACIÓN DE