Descargar este artículo en formato PDF
Perelló Roso, Ricardo y Gaspar Muñoz Cosme
2008 La bóveda Maya: Aportaciones para la excavación y conservación de las estructuras Mayas. En XXI Simposio de Arqueología en Guatemala, 2007 (editado por J.P. Laporte, B. Arroyo y H. Mejía), pp.1008- 1028. Museo Nacional de Arqueología y Etnología, Guatemala (versión digital).
64
LA BÓVEDA MAYA: APORTACIONES PARA LA EXCAVACIÓN Y CONSERVACIÓN DE LAS ESTRUCTURAS MAYAS
Ricardo Perelló Roso
Gaspar Muñoz Cosme
Universidad Politécnica de Valencia
Palabras clave
Arquitectura Maya, bóveda, estructuras, fórmulas de cálculo
Abstract
THE MAYA VAULT:
CONTRIBUTIONS FOR THE EXCAVATION AND PRESERVATION OF THESE MAYA STRUCTURES
In planning excavations and restoration work on Maya structures, it is critical to know in what kind of state the structures are in so as to determine the best measures to avoid collapse, as well as personal harm. The Maya arch or its approximation is the most widely used structural solution in all of the Maya area, as well as being a characteristic element of its architecture. In this work we propose a method of analysis based on their study by levels, which allows for a simple practical approach to understand the feature using geometric data to determine the actual state of these Maya arches.
Los trabajos de excavación y puesta en valor del patrimonio arquitectónico Maya presentan siempre la necesidad de trabajar en equipos multidisciplinarios en los que los diferentes especialistas puedan atender todas y cada una de las acciones que son necesarias para conseguir la recuperación en el mejor estado posible del bien patrimonial. La situación en que generalmente se encuentran los edificios que van a ser excavados, tras más de mil años de abandono y destrucción, precisa que se planifique previamente cuál va a ser el método y el sistema más adecuado para iniciar la excavación, tratando siempre de preservar la integridad de la arquitectura conservada.
Esto no es una labor fácil, ya que nos encontramos con edificios que raramente se conservan íntegros, que han perdido parte de sus bóvedas y muros y, por tanto, se encuentran en un estado muy precario, en una situación infinitamente peor respecto a su estado original.
Porque debemos pensar que cuando un edificio inicia un proceso de destrucción, generalmente por el abandono, pierde todas las virtudes que una buena arquitectura posee. El principio vitruviano del firmitas (firmeza o solidez) que es una virtud en general aplicable a la buena arquitectura Maya del periodo Clásico, queda disminuido tanto por la autodestrucción por erosión, como por los diferentes agentes externos medioambientales que incrementan esta destrucción. Cuando se inicia la excavación de un montículo hay que pensar que debemos que afrontar la intervención en un edificio, si se permite el símil, muchas veces mutilado o “enfermo” y que no se va a poder restituir en su integridad original. Pero además, es necesario aunar los esfuerzos de arqueólogos y arquitectos para poder deducir inicialmente, por los indicios que se pueden encontrar, cómo es el edificio que está oculto dentro del montículo y cuáles son sus características estructurales y tipológicas que puedan orientar al especialista para establecer un adecuado plan de intervención de la excavación, de forma que se puedan tomar todas las precauciones necesarias para que las partes conservadas del edificio no pierdan su integridad.
Es, por tanto, muy importante conocer cuál es la forma habitual en que estos edificios se han ido desmoronando con el tiempo, teniendo en cuenta que hay unos elementos más frágiles, tales como dinteles y vanos, que serán los primeros en ceder y cómo luego, la propia autodestrucción, puede ir acumulando el escombro y la tierra sobre el edificio, creando nuevos equilibrios estructurales muchas veces precarios.
Los sistemas constructivos Mayas tenían una eficacia estructural demostrada, pero también, como se ha indicado, poseían algunos puntos débiles. Además, era una arquitectura pensada para tener un sistema de mantenimiento continuo que reparaba y reponía todos los elementos de revestimientos y estucos que la protegían del medio natural y la erosión.
Hoy en día, nos encontramos con la desnudez de los edificios que se excavan, en donde todos los elementos de protección externa han desaparecido casi por completo, de forma que el agua y la vegetación han penetrado, originando a su paso destrucción y disgregación de los materiales internos y, por tanto, cambios sustanciales en los equilibrios estructurales originales; entonces, es necesario adoptar métodos que permitan conocer de la salud estructural de los edificios que serán excavados.
En este sentido, y desde el Grupo de Investigación que sobre temas de patrimonio cultural Maya trabaja en la Universidad Politécnica de Valencia, se ha planteado una investigación estructural sobre uno de los elementos fundamentales de la arquitectura Maya: la bóveda de aproximación.
LA BÓVEDA MAYA
Nos encontramos ante un elemento estructural singular por sus propias características de “falsa bóveda”, que permite algunos estados de equilibrios estables en donde se conserva solamente una de las dos partes de la bóveda. Y es así como muchas veces nos encontramos estas bóvedas en los edificios excavados.
En el momento en que comienzan los trabajos de estudio de un elemento arquitectónico, habitualmente se hace necesaria la determinación de su comportamiento estático y su mecanismo resistente, es decir, cuál es la manera que adopta el elemento constructivo para soportar las fuerzas (pesos propios, sobrecargas, etc.) que inevitablemente le afectan.
A partir de este conocimiento es posible dilucidar la necesidad o no de un análisis en profundidad que aporte datos del estado real del elemento como estructura resistente, tales como los valores admisibles de carga o el valor del coeficiente de seguridad real de la estructura, entre otros. Sólo a partir de un conocimiento preciso de estas cuestiones podemos definir la necesidad o no de intervenciones de refuerzo, siendo un valioso apoyo para definir cuál es la manera más efectiva para diseñar y ejecutar estas intervenciones, en el caso de que la intervención estructural sea necesaria.
El proceso habitual consiste en determinar, por una parte, el efecto producido por el estado de cargas más desfavorables haciendo mayor su efecto mediante un coeficiente de seguridad (Sd), y por otra el valor máximo de respuesta de la estructura, minorada por el coeficiente de seguridad correspondiente (Rd). Se considera que el comportamiento de la estructura es aceptable si la capacidad de respuesta es superior al estado de solicitaciones pésimo a que va a estar sometida la estructura: Sd ≤ Rd.
Para las estructuras convencionales de nueva planta existen procesos suficientemente probados para la definición de los valores, tanto de resistencia última como de solicitaciones de cálculo, que acortan el grado de incertidumbre sobre los resultados obtenidos.
Sin embargo, la definición de los valores e hipótesis que permiten el análisis del comportamiento estructural de un edificio histórico de fábrica es mucho más compleja que la de un edificio de nueva planta construido con los materiales y los sistemas constructivos actuales.
Los materiales de los edificios históricos adolecen, por lo general, de una gran falta de homogeneidad, algo necesario para definir algunos parámetros tan importantes para el cálculo como módulos de deformación longitudinal o los valores de resistencia de los materiales. Se trata, por tanto, de una labor compleja y los valores obtenidos no son siempre fiables.
En lo que se refiere a los sistemas constructivos, el comportamiento de las estructuras discretizables en elementos lineales (estructuras formadas por pilares y vigas) ha sido ampliamente estudiado a partir de las hipótesis establecidas por la Resistencia de Materiales clásica, tanto en su fase de comportamiento elástico como, de permitirlo el material, en la zona de comportamiento plástico del mismo. Las hipótesis aplicadas y los criterios a la hora de realizar los modelados sobre los que se efectúan los cálculos cuentan con una aceptación generalizada.
Con estructuras de estas características es con lo que se construye la gran mayoría de las estructuras en la actualidad, por lo que su comportamiento deviene intuitivo a poco que se trabaje en este ámbito. Su traslación a los materiales de un edificio histórico es prácticamente directa, y dado que, por lo general, se trata de estructuras de bajo grado de hiperestaticidad su análisis es habitualmente sencillo. El problema se encuentra en la definición precisa de algunos valores que tienen gran influencia en el cálculo, como las excentricidades de apoyos o los grados de empotramiento.
Los elementos superficiales y volumétricos (arcos, sistemas abovedados) requieren métodos de cálculo más complejos. Su comportamiento no es tan intuitivo, y la aceptación sobre los criterios de modelado y los métodos de cálculo a emplear, en el caso de estructuras históricas, no es tan unánime.
No obstante, en los últimos años, y gracias a métodos como el de análisis rígido plástico o el Método de los Elementos Finitos, se ha aumentado el conocimiento del comportamiento y modelado de estructuras continuas como bóvedas o arcos, construidas con materiales con respuesta no lineal y de baja resistencia a la tracción como las fábricas, si bien su aplicación al sistema constructivo de bóvedas de aproximación por hiladas no ha sido tan extensivo.
Por otra parte, en diversas fases de los trabajos de intervención en un sitio arqueológico puede ser conveniente, o incluso imprescindible, la comprobación del estado de un elemento arquitectónico para determinar la existencia o no de riesgo inmediato para la estructura o para los investigadores que estén trabajando en ella, que determine la necesidad de ejecución de obras de emergencia de apeo o consolidación de la misma.
El modelo estructural de las bóvedas de aproximación por hiladas, el más característico de los construidos por los antiguos Mayas, presenta importantes limitaciones, y quizá por ello ha sido menospreciado frente al arco y la bóveda, capaces de conseguir luces y espacios de mucha mayor magnitud a partir de medios técnicos similares. Sin embargo, en el ámbito Maya un gran volumen de edificaciones de enorme valor patrimonial está construido con este sistema.
Por otra parte, el predominio de la arqueología como método científico para el estudio de la cultura Maya y, por tanto, de su construcciones, ha hecho que el acercamiento a ellas desde el punto de vista del análisis estructural haya sido muy limitado, si no prácticamente inexistente hasta la actualidad. Si bien de un tiempo a esta parte los equipos de estudio se han ampliado, convirtiéndose en equipos interdisciplinarios que abarcan ámbitos de conocimiento cada vez mayores y aportan datos para lograr avanzar en una comprensión global de esta cultura. Dentro de este contexto se enmarca el presente trabajo.
En la presente versión digital se ha incluido una serie de fotografías y esquemas que apoyan las ideas vertidas en este trabajo (Figuras 7 a 17).
DEFINICIÓN TIPOLÓGICA
Existe una gran variedad formal de bóvedas de aproximación, y en atención a esta cuestión es cómo se han clasificado habitualmente.
Sin embargo, lo que caracteriza desde el punto de vista estructural a todos estos elementos es que el elemento de cierre entre las bóvedas de los dos muros enfrentados se dispone con su junta en horizontal, y por lo tanto no es perpendicular al correspondiente funicular de esfuerzos que aparecería en este punto en un arco o una bóveda convencional. El uso del término “tapa” para este elemento, en lugar del término “clave” que se da a la piedra de cierre de un arco, ejemplifica su escasa aptitud para la transmisión correcta de esfuerzos horizontales entre las dos caras de la bóveda, y la diferencia notable de comportamiento que se intuye entre estos dos sistemas estructurales.
ANÁLISIS DEL COMPORTAMIENTO ESTRUCTURAL DEL SISTEMA DE BÓVEDAS DE APROXIMACIÓN
Para el estudio del comportamiento de las estructuras de fábrica una buena opción es lo que se conoce como el “estudio por niveles”. Para ello se aborda el análisis estructural de manera múltiple, comenzando por niveles en los que se adoptan simplificaciones muy generales, y se aceptan resultados con un grado de exactitud bajo, pero como contrapartida se requieren muy pocos datos y pocos medios para realizar el cálculo.
A medida en que se avanza en los niveles de estudio éste reviste mayor complejidad y para su aplicación es necesario un mayor volumen de datos, por contrapartida la aproximación al comportamiento estructural es mejor.
En la definición de estos niveles es necesario garantizar que los resultados obtenidos en un nivel, si bien son menos afinados que los de los niveles superiores, están siempre del lado de la seguridad, de forma que para garantizar que el comportamiento de la estructura es aceptable, basta con llegar al primer nivel en el que se cumplan de forma satisfactoria las condiciones establecidas para ello.
Por otra parte, aplicar estos métodos empezando por los más sencillos y avanzando en su complejidad permite fundamentalmente avanzar en el conocimiento del sistema estructural obteniendo datos cada vez más precisos y más ajustados al comportamiento real de la estructura, además de calibrar las diferencias entre ellos, comparar sus resultados e incluso propiciar la redefinición de niveles inferiores si los datos obtenidos lo consideran necesario.
En el presente trabajo se ha hecho especial énfasis en la definición de los primeros niveles de estudio por un doble motivo. Por un lado, son los que mayores diferencias presentan entre el sistema de bóvedas de aproximación por hiladas y los ya utilizados habitualmente para las estructuras de arcos y bóvedas. Por otra parte, en determinadas situaciones, puede ser necesaria la utilización de métodos que proporcionen una fiabilidad lo suficientemente aceptable con medios escasos y con un volumen limitado de datos de partida. Por ejemplo, durante el proceso de excavación arqueológica puede ser conveniente realizar una primera aproximación que aporte datos del nivel de seguridad de las estructuras exhumadas, y que informen de la conveniencia o necesidad de apeos o refuerzos, al menos provisionales, e incluso de la urgencia de una intervención.
Una vez definidos estos niveles se ha procedido a su comprobación mediante la aplicación de niveles superiores, en concreto de la aplicación del Método de los Elementos Finitos, obteniéndose una aproximación aceptable y del lado de la seguridad, por lo que se ha considerado que las hipótesis a partir de las que se han definido los niveles bajos de estudio son correctas.
La introducción de los procesos numéricos de cálculo, especialmente el Método de los Elementos Finitos, permite la obtención de la respuesta mecánica de elementos másicos con gran precisión y permite introducir hipótesis de comportamiento del material muy complejas, pero necesita de una mayor cantidad de datos y de sistemas informáticos capaces de resolver el gran volumen de operativa que se genera.
Los niveles de estudio propuestos son cuatro. Un primer nivel de equilibrio como sólido rígido, en que se estudia la estabilidad del conjunto; un segundo nivel con análisis en rango elástico del material con análisis tensional, admitiendo una cierta respuesta del material frente a esfuerzos de tracción; un tercer nivel, con análisis rígido plástico y comportamiento unilateral del material, y un último nivel de análisis por el Método de los Elementos Finitos en rango elástico.
Para estas primeras fases de análisis se ha despreciado la contribución de las posibles fuerzas de estabilizadoras provocadas por la transmisión de esfuerzos horizontales entre las dos caras de la bóveda. Es por ello que en estos niveles se ha calculado el comportamiento estructural de un solo lateral. Dada la solución constructiva con la que se han ejecutado estos elementos, la aparición de una fuerza equilibrante horizontal sólo sería posible movilizando las fuerzas de rozamiento que impidan el deslizamiento entre tapa y cara superior de los lados de las bóvedas. Si bien esto es hipotéticamente posible, la realidad de los restos existentes en toda el área Maya parece indicar que en una gran parte de estructuras esta fuerza estabilizadora no se genera o deja de actuar en algún momento. Una parte importantísima de los edificios están en la actualidad en ruina parcial, conservando uno de los dos laterales de la bóveda en pie.
Por otra parte, es evidente que el estudio de cada lateral de la bóveda como elemento independiente está claramente del lado de la seguridad, por lo que en niveles bajos de estudio garantiza la eficacia pericial de un diagnóstico favorable.
Los materiales que forman la fábrica son de gran homogeneidad, ya que toda la piedra utilizada, tanto para sillares como para mampuestos, proviene de la misma cantera. A su vez, los morteros están realizados a partir de la calcinación de los ripios resultantes de la extracción de la piedra de los muros, por lo que para la estimación de cargas y el posicionado de resultantes se ha considerado como hipótesis que todo el volumen de la bóveda está ejecutada con un material uniforme, y por tanto igual peso específico.
Como se verá en la definición de estos niveles, los datos utilizados o bien son muy sencillos de obtener, o bien se pueden estimar de forma aproximada sin influir, en la mayor parte de los casos, de manera decisiva en el cálculo.
ANÁLISIS POR EQUILIBRIO
El estudio global con el volumen completo supone una primera aproximación al problema, que aunque no es generalizable para todos los casos, puede suponer para determinadas situaciones una aproximación aceptable. Supone calcular la resultante total de masas y el punto de paso de la misma.
Si la resultante total pasa por dentro del núcleo central (es decir por el tercio central) del muro de soporte de la bóveda, todas las secciones trabajan comprimidas, por lo que la aproximación es buena. En este caso la estabilidad frente a acciones gravitatorias está garantizada.
Si la resultante es exterior al núcleo central es necesaria la comprobación de los niveles superiores.
Como se verá, se trata de un dimensionado en que los únicos datos utilizados son la definición geométrica de la bóveda (Figuras 1a, 1b, 1c).
ANÁLISIS SECCIONAL EN RANGO ELÁSTICO DEL MATERIAL
Por su sencillez en el análisis se ha introducido el estudio como sólido con comportamiento lineal y elástico del material, mediante un análisis seccional de la estructura.
Tanto el axil solicitación como la excentricidad del mismo son conocidos para cada una de las secciones de estudio, por lo que la obtención de la distribución de tensiones normales puede realizarse con las expresiones clásicas de la resistencia de materiales para una sección sometida a solicitaciones de flexión compuesta, por lo que la obtención de las tensiones normales máximas es inmediata.
A partir de los valores obtenidos se comparan los máximos valores de tensión, tracción y compresión con los valores de cálculo del material, admitiendo un cierto valor en las tensiones de tracción del mismo, definido por un porcentaje de la resistencia a compresión del material.
Es obvio que para que esta capacidad de respuesta a tracción de las fábricas realmente exista, será necesaria la colaboración de morteros de junta de buena calidad y que el estado de conservación de la fábrica sea tal que no se haya producido la disgregación o el lavado de estos morteros.
Los datos necesarios para realización de este nivel de análisis son la definición geométrica de la bóveda, el peso específico del material, y la resistencia de cálculo de la fábrica. En general, con definir valores tipo aproximado para las densidades y las resistencias es suficiente, ya que los valores que se obtienen para los estados tensionales en las secciones son muy bajos.
El límite de validez del nivel viene generalmente dado por la resistencia a tracción de las fábricas. Por otra parte, el análisis en diferentes rebanadas permite obtener el punto en que aparecen las primeras tensiones de tracción en el material, por lo tanto, de no aceptarse éstas, aparecerían las fisuras en los riñones de la bóveda.
ANÁLISIS RÍGIDO-PLÁSTICO CON COMPORTAMIENTO UNIDIRECCIONAL DE MATERIAL
Para este nivel de análisis se ha utilizado la hipótesis del análisis rígido-plástico con comportamiento unilateral del material, ampliándolo a un estudio seccional de la sección.
El análisis rígido-plástico, basado en la teoría desarrollada por Jacques Heyman (1995) a partir de la década de los sesenta, en especial para arcos, aplica las hipótesis fundamentales de la plasticidad sobre un modelo de comportamiento del material en que se supone un comportamiento infinitamente resistente de la fábrica a compresión y nula a tracción.
En realidad, para casi todas las obras de fábrica se comprueba que los esfuerzos de compresión sobre los materiales pétreos quedan claramente por debajo de su límite de rotura, y lo que puede producir el colapso es la aplicación excéntrica de las cargas sobre la sección.
En esta hipótesis, la resultante ha de pasar necesariamente dentro de la sección para que se produzca el equilibrio. Sin embargo, admite la existencia de centros de presiones (puntos de aplicación de la resultante) exteriores al núcleo central de la sección (el tercio central en el caso de secciones rectangulares). En el caso extremo, cuando la resultante sea tangente a la sección, ésta será capaz de transmitir los esfuerzos de compresión, pero no de impedir el giro. Heyman (1995) asimila el comportamiento de estas secciones a las rótulas plásticas descritas para los materiales con comportamiento dúctil, por ejemplo el acero, y sobre esta hipótesis de comportamiento aplica los teoremas fundamentales de la plasticidad.
Esta hipótesis se aproxima al comportamiento esperable de la estructura, sobre todo en aquellos casos en que los morteros de junta son especialmente pobres o inexistentes, y ha servido para aclarar el comportamiento de arcos y bóvedas y su relación con los estribos y contrafuertes.
Cuando se trata de un muro con sólo uno de los laterales de bóveda, el modelado es el equivalente a un voladizo con el empotramiento en suelo, por lo que es evidente que el colapso se produce con una única rótula. El punto crítico es habitualmente el encuentro de la bóveda con el muro, donde la excentricidad suele ser máxima.
Hay que hacer notar que si bien en el caso de arcos, el hecho de que la carga sea exterior al núcleo central de la sección resistente no tiene influencia en la definición del funicular de esfuerzos ni en la magnitud de la resultante, en el caso de muros inclinados o de bóvedas falsas y debido al modelo de comportamiento unilateral, sí puede tenerla. El hecho de que la resultante salga fuera del núcleo central provoca la fisuración de la sección hasta el eje neutro. El volumen que queda por fuera de la fisura ya no será computable a nivel de masa para equilibrar el momento de vuelco, por lo que será necesario volver a definir la resultante y el punto de paso de la misma a partir de este momento.
Este método evalúa la estabilidad exclusivamente con parámetros geométricos, ya que en las hipótesis iniciales se suponen valores infinitos de resistencia. Sin embargo, establecida una hipótesis de respuesta es posible determinar el estado tensional de las secciones más desfavorables, bien con las fórmulas generales de la resistencia de materiales, bien con las expresiones aproximadas de la sección cobaricéntrica.
La gran ventaja de este nivel de análisis es que se puede realizar con muy pocos datos, y puede ser suficiente para comprobar la estabilidad de tipos estructurales sencillos, a partir de pocos medios y con fiabilidad, ya que las hipótesis efectuadas están del lado de la seguridad.
Las hipótesis a partir de las que se define el modelo de cálculo en este nivel son las siguientes.
COMPORTAMIENTO UNIDIRECCIONAL DEL MATERIAL
Como cualquier material pétreo, las fábricas presentan buen comportamiento frente a esfuerzos de compresión. Sin embargo frente a esfuerzos de tracción la respuesta es deficiente, presentando fracturas frágiles con valores muy bajos de tensión.
El sistema constructivo empleado acentúa este efecto, la cara solicitada con esfuerzos de compresión, el intradós, es la ejecutada con la fábrica más resistente, y la menos comprimida, o en su caso traccionada, el trasdós, está ejecutada con la fábrica de menor resistencia.
Así pues, en el cálculo se ha considerado que la respuesta de la sección se produce únicamente en la zona comprimida, con respuesta nula en la zona de tracción.
A pesar de lo dicho, y atendiendo a la calidad y factura de las fábricas, esta hipótesis cae del lado de la seguridad en la mayor parte de los elementos con buen estado de conservación. En el caso de estructuras con procesos de disgregación avanzados parece la hipótesis más ajustada a la realidad.
RESISTENCIA INFINITA DE LA FÁBRICA FRENTE A ESFUERZOS DE COMPRESIÓN
En un primer estadio del análisis, a la hora de evaluar el equilibrio, sólo se ha tenido en cuenta el efecto del vuelco del sólido, independientemente de la resistencia del material.
Evidentemente el paso de la resultante cerca del borde libre de la pieza implica un incremento considerable de las tensiones de compresión, que podrían conducir a un colapso del material. Es importante hacer notar que, a diferencia de lo descrito para el análisis rígido plástico de arcos, aquí no es factible la plastificación de la sección. En un arco, el aplastamiento del punto de giro supone un aumento de la sección de contacto, por lo tanto una redistribución de las tensiones sin una variación considerable en la posición del punto de paso del antifunicular de esfuerzos. Por el contrario, en el caso de bóvedas por avance sucesivo de hiladas, al igual que en el caso de vuelco de muros, una concentración de tensiones en el punto de giro que suponga el colapso del material y el aumento de la superficie de contacto, desplaza la resultante de respuesta hacia el interior del muro, aumentando el momento de vuelco, haciendo inviable el equilibrio.
Por todo ello con posterioridad al estudio de equilibrio, y en los casos en que la resultante pase cerca del borde libre, es necesario proseguir el análisis con un estudio tensional.
MÉTODOS DE CÁLCULO
Para estos tres niveles de análisis el proceso se ha realizado en una primera instancia de forma gráfica. El cálculo gráfico, sin embargo, presenta el problema de su falta de agilidad, por ello se ha realizado una rutina informática que realiza los cálculos para este tipo de estructuras, con las hipótesis descritas, y a partir de un número muy limitado de datos.
Las expresiones matemáticas se definen a partir de un sistema de referencia cuyo origen se sitúa en el eje de la parte inferior de la tapa, necesitándose como datos de partida los que fijan la geometría básica en sección de la bóveda y los referentes al comportamiento del material (Figura 2).
A partir de estos datos se establecen las ecuaciones de equilibrio en una sección genérica i, obteniéndose la resultante de cargas verticales a partir del equilibrio de fuerzas y la posición de la misma a partir del equilibrio de momentos.
Para fijar estos valores es necesario conocer las funciones matemáticas y=f(x) que definen las caras del macizo de la bóveda.
En el caso de las bóvedas del periodo Clásico Maya de la zona de Petén, en una gran mayoría se trata de superficies planas. Por ello, la relación de las abscisas y ordenadas de la traza de la bóveda en la sección se trata de una recta. En atención a la metodología utilizada para la toma de datos del volumen, parece inmediato caracterizar la recta que genera el intradós por sus dos puntos más significativos, el arranque (punto A del gráfico) y su extremo volado (punto B), y por dos puntos cualesquiera para la recta del trasdós, con lo que queda fijado el volumen a computar para la definición de masas.
La rutina obtiene los puntos x1 y x2 límite de la cada rebanada de manera automática en el caso de intradós y trasdós rectos, permitiendo la introducción por coordenadas en el resto de los casos.
En el momento en que la resultante de cargas sea exterior al núcleo central de la sección (en el caso de secciones rectangulares el tercio central), el eje neutro corta la sección. En este caso, y en modelos de comportamiento unidireccional del sólido, se genera una fisura hasta el eje neutro, por lo que la parte de sección sin compresión, no sólo deja de colaborar en el equilibrio tensional, sino también deja de aportar masa que colabore en el centrado de la resultante.
A partir de este punto, la definición del límite exterior de la rebanada deja de ser el trasdós, formando una nueva curva x’2.
Del equilibrio de fuerzas sobre la sección, y a partir de una distribución de tensiones en cuña triangular, podemos definir profundidad de la fisura, y por tanto la x’2 que nos indica la dimensión computable del tramo i, y el punto de paso de la resultante.
A partir de este momento se pueden definir las comprobaciones a realizar.
EQUILIBRIO GLOBAL DEL SÓLIDO
Este equilibrio ha de extenderse a todas las rebanadas. Será necesario imponer que la resultante de cada sección pase dentro de la sección inferior.
Para garantizar el equilibrio global del volumen de la bóveda como sólido rígido será necesario imponer que la resultante en la sección del apoyo sobre el muro pase dentro de éste, siendo ésta, debido a su configuración geométrica, la más desfavorable.
COMPROBACIONES TENSIONALES
La comprobación frente a tensiones normales se realiza para una respuesta suponiendo que se cumple la hipótesis de Navier-Bernouilli (planeidad de secciones) y con proporcionalidad entre tensiones y deformaciones, es decir para una cuña de tensiones normales en la sección que sigue la ley de Navier (Figura 3).
En el análisis con comportamiento unidireccional del material se han tomado como valores de área, módulo resistente y excentricidad, los correspondientes a la sección fisurada, por lo que los valores de tensión resultante en la zona menos comprimida corresponden a la curva de fisuración, y por lo tanto son nulos.
Si bien esta hipótesis es la más conservadora, ya que no contempla la posibilidad de cargas de centrado introducidas en la estructura completa por fuerzas de rozamiento entre tapa y bóveda ni la capacidad de resistencia a tracción del material, un resultado favorable hablaría de un comportamiento aceptable de la estructura frente a cargas verticales, incluso en el caso de estructuras incompletas y con sus fábricas en estado de deterioro importante.
En la rutina de cálculo se ha realizado un esquema gráfico de las rectas de intradós, trasdós y curva de fisuración (Figuras 4, 5 y 6).
ANÁLISIS MEDIANTE EL MÉTODO DE LOS ELEMENTOS FINITOS
Para analizar la fiabilidad de las hipótesis adoptadas en los niveles de cálculo anteriores, se ha realizado un estudio mediante el Método de los Elementos finitos en una rebanada de estructura con las mismas características geométricas y mecánicas a las calculadas en los niveles anteriores, obteniéndose una buena aproximación con los valores obtenidos en los niveles inferiores.
Los valores tensión obtenidos mediante el MEF son de orden de magnitud muy similar a los obtenidos en el nivel de estudio correspondiente al estudio seccional de la pieza con admisión de tracciones, pero de valor ligeramente inferior.
REFERENCIAS
Heyman, Jacques
1995 Teoría, historia y restauración de Estructuras de Fábrica. Ministerio de Obras Públicas Transporte y Medio Ambiente, Madrid.
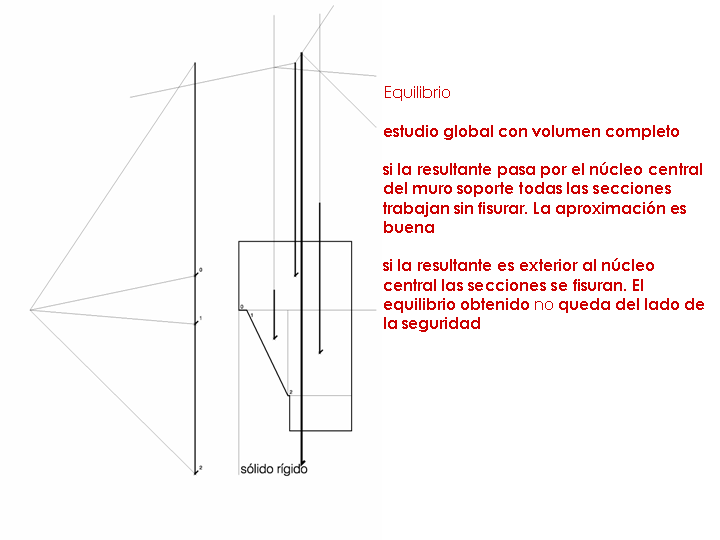
Figura 1a Análisis del primer nivel mediante método gráfico
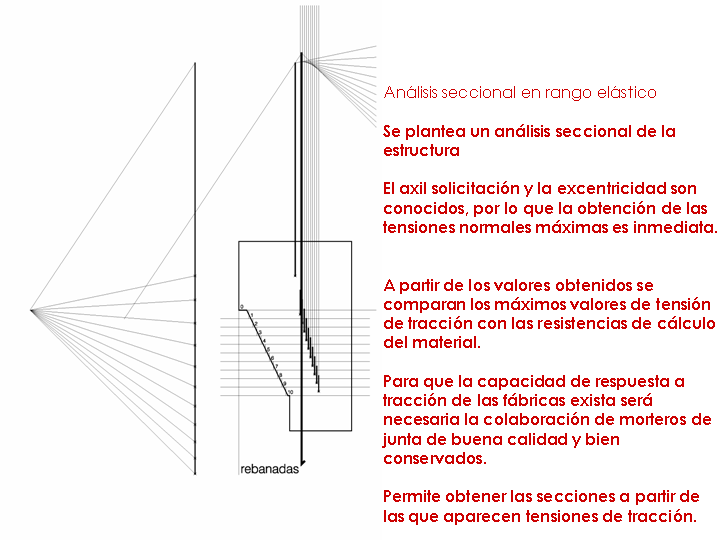
Figura 1b Análisis del segundo nivel mediante método gráfico

Figura 1c Análisis del tercer nivel mediante método gráfico

Figura 2 Definición geométrica de la bóveda

Figura 1 Centro de presiones y distribución de tensiones normales en la sección sin fisurar

Figura 4 Rutina de cálculo. Entrada de datos

Figura 5 Rutina de cálculo. Análisis en comportamiento unidireccional

Figura 6 Rutina de cálculo. Gráfico de fisura

Figura 7 Edificio Maya

Figura 8 Edificio Maya

Figura 9 Bóveda

Figura 10 Edificio Maya

Figura 11 Bóveda

Figura 12 Bóveda

Figura 13 Bóveda

Figura 14 Bóveda

Figura 15 Bóveda

Figura 16 Dibujo histórico de bóveda

Figura 17

